- Sphere Engine overview
- Compilers
- Overview
- API
- Widgets
- Resources
- Problems
- Overview
- API
- Widgets
- Handbook
- Resources
- Containers
- Overview
- Glossary
- API
- Workspaces
- Handbook
- Resources
- RESOURCES
- Programming languages
- Modules comparison
- Webhooks
- Infrastructure management
- API changelog
- FAQ
This section provides a further and deeper understanding of many aspects of the process for creating programming problems. Despite being outside the main body of the handbook the information contained here should provide the key to many issues raised in the main section.
Good test cases design
There is a common problem that leads to bad test case design. This is the prevalent process of creating a huge amount of small test cases instead of one large test case. For this reason, the system limits the number of test cases assigned to a problem, so it is not possible to create a large number of them. The individual test case is not intended to test only a single set of data for the programming problem.
Tip: We recommend that you redesign your input and output specification to deal with multiple sets of data within a single test case.
Consider the following elementary problem as an example:
For a given integer numbers
aandbcalculate the suma + b.
The first approach to the input and output specification is to require a calculation of the sum only for two numbers:
Input specification
In the only line of the input file, there will be two integer numbers a and b separated by a single space character.
Output specification
Your program should write a single number which is the value of a + b.
Examples
Input 2 3 Output 5Input -1 1 Output 0Input 10 11 Output 21Test cases
Test case Input file Output file 1
(example data)2 3 5 2
(example data)-1 1 0 3
(example data)10 11 21 4 95 -36 59 5 45 -12 33 6 46 -89 -43 7 19 16 35 8 -91 -10 -101 9 -45 3 -42 10 -38 -90 -128 11 41 -52 -11 12 -52 78 26 13 -37 -58 -95 14 20 2 22 15 89 21 110 16 39 37 76
This is a correct approach, but it is especially not recommended - especially due to the ineffective use of resources. In addition, even the maximum number of test cases allows us to cover a small part of the possible data sets. Therefore, the verification isn't as comprehensive as it could (and should) be.
The following input and output specification presents an alternative approach that is recommended for Sphere Engine Problems service as well as any other Online Judge systems. Using this approach you can pack a large number of data sets into a single test case.
Input specification
In the first line, there will be a single integer
Twhich is the number of data sets for the problem defined in the task description. In each of the nextTlines, there will be a pair of two numbersaandbfor which you should calculate the suma + b.Output specification
For each
a, bpair print the calculated suma + b. Separate answers with a newline character.Example
Input 3 2 3 -1 1 10 11 Output 5 0 21Test cases
Test case Input file Output file 1
(example data)3
2 3
-1 1
10 115
0
212 13
95 -36
45 -12
46 -89
19 16
-91 -10
-45 3
-38 -90
41 -52
-52 78
-37 -58
20 2
89 21
39 3759
33
-43
35
-101
-42
-128
-11
26
-95
22
110
76
Of course, the second test case in the above example can contain even millions of data sets (now it contains 13 data sets). This is a huge advantage of the recommended approach comparing to the poor problem design presented before.
Tip: Multiple test cases should be used to test different aspects of a solution's correctness regarding the programming problem (e.g., border cases, efficiency, etc.).
Interactive problems
The standard schema of the submission processing assumes that at first the execution of the user's program generates the user's output and after that, the test case judge in a certain way compares it with the model output. In the interactive problem, these phases are executed simultaneously.
The execution of the user's program starts and its standard output is directed to the test case judge as its standard input. At the same time, the test case judge program starts and its standard output is directed to the user's program as its standard input. This allows for direct communication between the user's program and the test case judge as you can see in the diagram below.
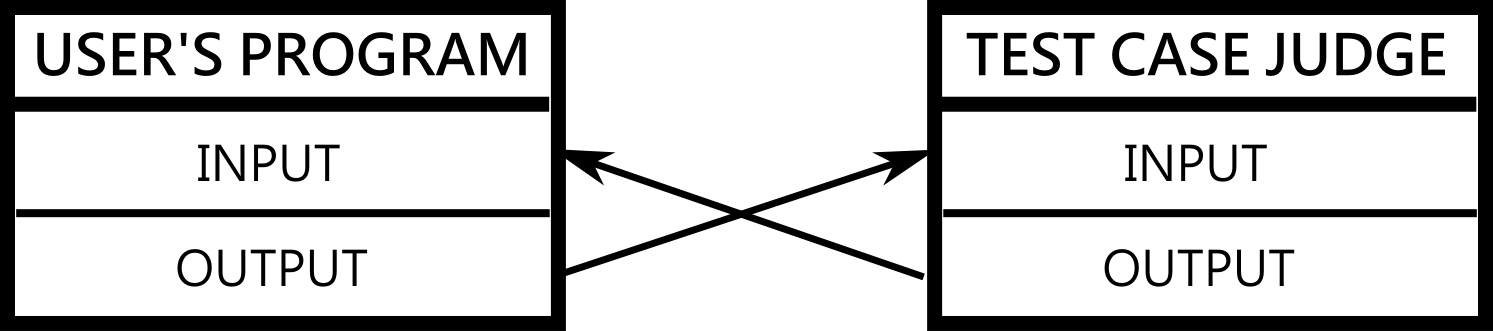
Important: The interactive problem requires a dedicated test case judge adjusted to the specifics of the communication with the user's solution.
When the communication is open, the test case judge can interactively generate input for the user's program depending on its output. At the same time, it is possible to verify the correctness of the results delivered by the user's program.
Write a program that will win the chess game with the opponent who makes random legal moves.
Input
The first line of the input contains the number
swhich can be0or1. Ifs = 0, then your opponent plays white pieces and ifs = 1then you play white pieces.In the next lines, there will be moves of your opponent written in the standard chess algebraic notation (for example
e4 e5means that the piece one4moves toe5). You can assume that all opponent moves are legal. When the match is over the final line of the input will be "WIN" or "LOSE". Your solution will be accepted if it wins the match.Output
If
s = 1you start with the first move (i.e., you write the line with your move in the standard chess algebraic notation). After that, you write your next move after you get your opponent's move and so on and so forth. Ifs = 0you wait for your opponent's move and then again you play move by move.
By the description given in this example you can see that it is required to implement the test case judge, which is able to play a random chess game:
- it remembers the state of the chess board,
- it can make legal moves,
- it can verify that the game is over and who the winner is,
- it accepts only solutions that will win the game.
Important: Due to input and output processing optimizations used in most programming languages, it is highly recommended to clear the output buffer after printing each line. This should be applied in both: test case judge and user's solution.
For example, in C language it can be done by using the fflush(stdout) command.
Time complexity
The properly designed test cases with adjusted time limits provide a possibility
of verification of the time complexity of algorithms used in the user's
solutions. Let's consider the basic case when the content manager knows two
different algorithms for a programming problem, say A and B. Let's assume
that the algorithm A is significantly faster than the algorithm B.
Assuming that we have input data which is processed in the time
tA for the algorithm A which is much faster than
execution time tB for the algorithm B - we can simply
set the time limit somewhere between those values.
Note: The computation speed depends on the machine that runs the user's program. Test cases dedicated to testing efficiency should be designed to be compatible with machines that execute programs.
With the timeout tA ≤ t0 ≤ tB we
can assume that A-like algorithms will pass the test case and B-like
algorithms will fail due to exceeding the time limit.
Important: The presented method is not a real complexity testing. The slower algorithm can beat the faster one when it is technically optimized for the test cases and the machine.
It is also not a universal method - changing the machine can allow slower algorithms to pass test cases designed for faster algorithms only.
Nevertheless, this is a very effective approach for well-designed test cases.
The sorting problem is one of the most demonstrative examples when there are
many different solutions. Most natural solutions need approximately
n2 operations to sort the sequence of length n.
However, the more sophisticated algorithms guarantee approximately n log(n)
operations, which is a significantly better result.
In the Example of Programming Problem
chapter, you can see properly prepared test cases which distinguish solutions
for The initial sum problem.
Important: For problems with multiple (not only two) solutions of different efficiency you can design a hierarchy of test cases to reflect the gradation of solutions using score.
Memory complexity
Similarly to time complexity testing, it is
possible to test the memory complexity of algorithms. Consider the simplest
situation when the content manager knows two different algorithms for a problem,
say A and B. We shall assume that algorithm A consumes a small and
constant amount of memory and algorithm B memory needs are dependent on the
problem input data (possibly big amounts).
You can distinguish between solutions A and B by constructing adjusted test
cases. If we denote that designed test case makes algorithm A use
mA megabytes of memory and algorithm B use
mB megabytes of memory and these values are fairly
separated you can set the memory limit m0 megabytes
somewhere between mA and mB.
Important: We do not directly support a memory limit option in the programming problem configuration panel due to differences between memory consumption for various programming languages. For example, every solution written in Java reports memory consumption that includes memory consumed by JVM.
In accordance with the note above you have to address the problem of limiting available memory that the program can use individually. As we said there is no single parameter which defines the memory limit. To obtain desired functionality you can construct a custom master judge (see Implementation of the master judge section of the Custom Judges chapter) and limit the memory inside separately for each programming language allowed for solutions.
The
prime numberproblem can be solved in a constant memory by looking for divisors. Alternatively, it can be solved with Sieve of Eratosthenes algorithm which consumes the amount of memory which depends on the input data.
Verdicts
There are two levels when the verdict is assigned to the submission:
- test case - the verdict is produced by the test case judge,
- master judge - the verdict is a combination of verdicts from test cases.
The master judge is responsible for summarizing the results of individual test cases. Based on partial results it determines the final verdict (and other parameters of the final result). As it is done arbitrarily, we will focus on the test case verdicts which have well-defined immutable meaning.
We separate verdicts into two groups: system verdicts and test case judge verdicts. The system verdicts are set by the system in case of interrupted execution of the user's solution. In contrast, the test case judge verdicts are set by the test case judge after successful execution.
- accepted (AC) - the submission is a correct solution to the programming problem,
- wrong answer (WA) - the program is executed correctly, but it is not a correct solution.
- time limit exceeded (TLE) - the submission execution took too long (i.e. longer than time limit defined for the test case),
- run-time error (RE) - an error occurred during program execution:
- NZEC (Non-Zero Exit Code) main function returned error signal (for example main function in C/C++ should return 0),
- SIGSEGV the program accessed unallocated memory (segmentation fault),
- SIGABRT the program received abort signal, usually programmer controls it (for example when C/C++
assertfunction yieldsfalse),- SIGFPE the floating point error, usually occurs when dividing by
0,- compilation error (CE) - an error occurred during compilation or syntax validation by the interpreter,
- internal error (IE) - an unexpected error occurred on the service side,
- judge error (JE) - test case judge or master judge error,
- problem error (PE) - problem configuration error.
Note: The internal error covers a wide area of various errors (including server errors).
The judge error covers a variety of issues related to test cases judges and master judges. For example:
- compilation error,
- output data format error,
- time limit exceeded,
- run-time error,
- incorrect
exit_code.
The problem error indicates an issue related to programming problem configuration, for example missing test cases.
To illustrate possible verdicts we shall again consider the following example:
For a positive integer n calculate the value of the sum of all positive integers that are not greater than
ni.e.,1 + 2 + 3 + ... + n. For instance whenn = 5, the correct answer is15.Input specification
In the first line is the number
1 ≤ T ≤ 10000000, which is the number of instances for your problem. In each of the nextTlines, there will be one numbernfor which you should calculate the defined initial sum.Output specification
For each
nprint the calculated initial sum. Separate answers with the newline character.
Source code
long long initsum(long long n) { return n*(n+1)/2; } int main() { int t // <------ missing semicolon long long n; scanf("%d", &t); while (t > 0) { scanf("%lld", &n); printf("%lld\n", initsum(n)); t--; } return 0; }The result
Test case Verdict Score Time Memory 1 compilation error 0 0s 0kB Final result compilation error 0 0s 1000kB
Source code
long long initsum(long long n) { return n*(n+1)/2; } int main() { int t; long long n; scanf("%d", &t); while (t > 0) { scanf("%lld", n); // <---- reference to unallocated memory printf("%lld\n", initsum(n)); t--; } return 0; }The result
Test case Verdict Score Time Memory 1 runtime error 0 0s 0kB Final result runtime error 0 0s 0kB
Source code
long long initsum(long long n) // <------ suboptimal algorithm { int i; long long sum = 0; for (i=1; i <= n; i++) { sum += i; } return sum; } int main() { int t; long long n; scanf("%d", &t); while (t > 0) { scanf("%lld", &n); printf("%lld\n", initsum(n)); t--; } return 0; }The result
Test case Verdict Score Time Memory 1 time limit exceeded 0 1.01s 1000kB Final result time limit exceeded 0 0s 0kB
Source code
long long initsum(long long n) { return n*(n+1); // <------- wrong formula } int main() { int t; long long n; scanf("%d", &t); while (t > 0) { scanf("%lld", &n); printf("%lld\n", initsum(n)); t--; } return 0; }The result
Test case Verdict Score Time Memory 1 wrong answer 0 0.01s 1000kB Final result wrong answer 0 0s 0kB
Source code
long long initsum(long long n) { return n*(n+1)/2; } int main() { int t; long long n; scanf("%d", &t); while (t > 0) { scanf("%lld", &n); printf("%lld\n", initsum(n)); t--; } return 0; }The result
Test case Verdict Score Time Memory 1 accepted 0 0.01s 1000kB Final result accepted 0 0.01s 1000kB
